Viaje locuelo a otras dimensiones con Monte Carlo
Hace poco publiqué una entrada sobre los métodos Monte Carlo en El zombi de Schrödinger, entrada que tuvo su réplica en El escriba matemático, explicando la pequeña locura que fue mezclar Python y Geogebra 5 en fase beta. De estos dos posts surgió esta animación de cálculo del número PI:
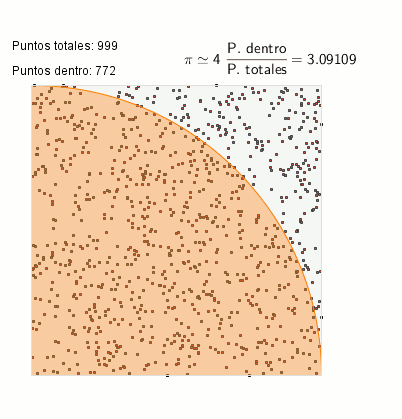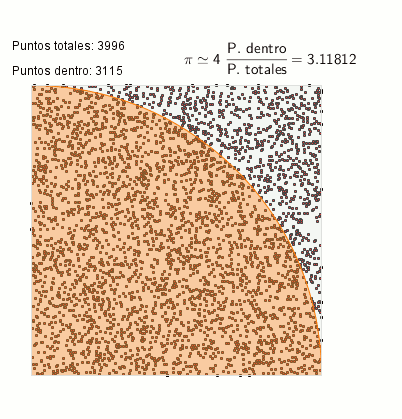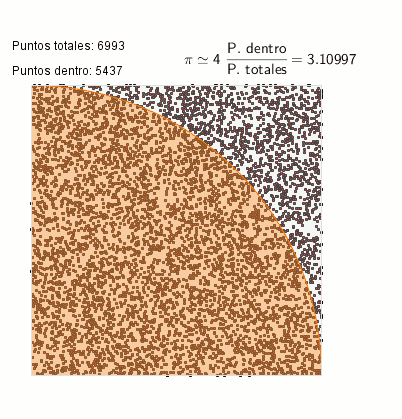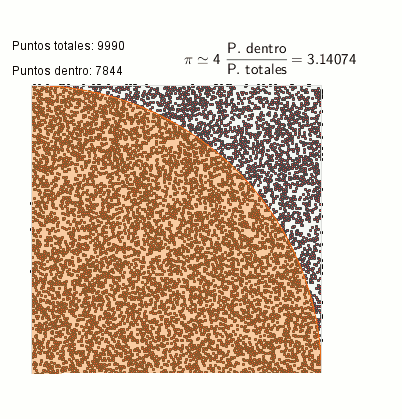
Cálculo de PI mediante el método Monte-Carlo
Pero ¿se puede afinar más en la búsqueda del número PI por este método? La respuesta es un SÍ rotundo. Una característica importante a la hora de ejecutar un método Monte Carlo es realizar una buena elección del generador de números aleatorios, cosa que no hice.
El cálculo de PI es un ejemplo de integración mediante método Monte Carlo: calculamos el área del sector del círculo y, gracias a la relación entre el área de ese sector y del cuadrado que lo contiene, obtenemos la aproximación de PI.
El área del cuadrado será
y el área del sector será
Si dividimos el área del círculo por el área del sector, tendremos:
Si realizamos la división del número total de puntos que tenemos dentro del círculo respecto al número total de puntos que se han señalado en toda la área del cuadrado, tendremos una aproximación del valor de π
En este tipo de problemas, un buen generador de números aleatorios será aquel que consiga cubrir el espacio estudiado lo más homogéneamente posible. De esta forma, habrá más probabilidad de que la razón entre el total de puntos lanzados y los puntos dentro de nuestro objeto sea similar a la razón real entre el volumen de nuestro campo de pruebas y el objeto circunscrito que deseamos medir.
Investigando el tema, descubrí un generador de números pseudoaleatorios llamado secuencia de Sobol (más información aquí) y que distribuye puntos de una forma muy homogénea a lo largo de las dimensiones que elijamos. A continuación, un ejemplo de una distribución de puntos obtenida uniformemente y otra obtenida mediante una secuencia Sobol:
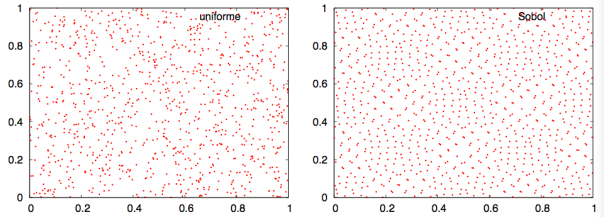
Comparativa de la generación de 1000 puntos aleatorios mediante el generador uniforme de python y la secuencia Sobol
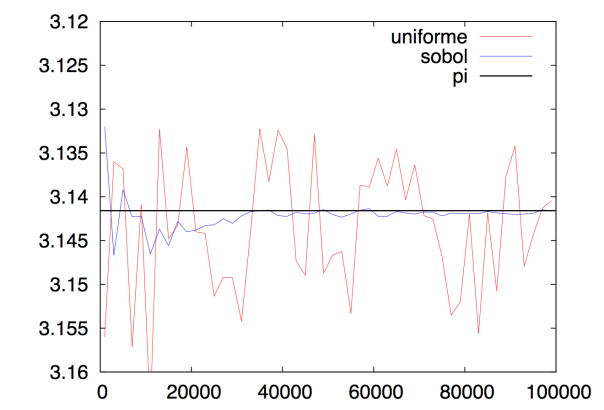
Lo siguiente fue comprobar si realmente se notaba la diferencia al realizar el cálculo de PI usando un método u otro. Aquí tenéis la comparación del cálculo de PI con un generador uniforme de números aleatorios y con un generador de secuencias Sobol:
El cálculo se realizó para distintos números de puntos lanzados, hasta un máximo de 100.000 puntos. Se puede ver con claridad la mejora que produce el uso de una secuencia Sobol (azul) respecto a un generador de números aleatorios uniforme. La convergencia hacia el valor de PI es muy evidente cuando usamos secuencias Sobol. Para ver el código fuente usado puedes ir a la parte final.
¿Por qué conformarnos solo con dos dimensiones?
Poco después descubrí un enlace a un artículo ya con solera de Gaussianos:
¿Cuál es el volumen de la bola unidad de dimensión N?
Grosso modo lo que nos cuenta es el particular comportamiento del volumen de una esfera de radio 1 a medida que aumentamos el número de dimensiones. Podemos ver cómo en principio el volumen aumenta con el número de dimensiones para luego decrecer, tendiendo hacia cero a medida que aumentamos n. La fórmula para el volumen de una n-esfera de radio 1 es:
La explicación es bastante lógica; para que un punto del espacio de n-dimensiones se encuentre dentro de la n-esfera de radio 1 correspondiente, debe cumplir que su distancia al origen sea menor o igual a 1, y a medida que aumentamos las dimensiones llega un momento en el que es muy difícil encontrar puntos que cumplan esta condición, ya que para cada dimensión tenemos que sumar el cuadrado de un nuevo término.
La fórmula para saber si un punto está dentro de una n-esfera es:
La rabia del asunto es que es imposible visualizar una n-esfera de más de tres dimensiones dentro de un cubo, a su vez, de n-dimensiones. Quizás sea imposible imaginarlo, pero una computadora sí que puede ayudarnos a hacer algo similar: podemos calcular aproximadamente el volumen de una n-esfera de la misma forma que hicimos antes con el área de un círculo. Así que toca lanzar n-puntos a cascoporro para meter el dedo en la yaga y ver si todo esto es cierto.
Para cada dimensión, el cálculo del volumen de la n-esfera de radio 1 será el siguiente:
Siendo el volumen del n_cubo: ya que cada arista del cubo tendrá longitud 2: [-1,1].
El código para realizar el cálculo sería el siguiente:
#Calculo del volumen de una n-esfera. Como parametro recibe el numero de dimensiones y de puntos a generar, como salida devuelve el volumen
def calc_n_sphere_sobol(n_dimensions, n_points):
#numero de puntos dentro de la n-esfera
hits = 0
#inicializador de la secuencia sobol
sout = random.randint(1,10000)
for i in range(0, n_points):
#generar punto n-dimensional
p, sout = sobol_lib.i4_sobol ( n_dimensions, sout )
#transforma el numero del intervalo [0,1] al intervalo [-1,1]
p = (p*2)-1
j = 0
s = 0
#sumar cuadrado de las componentes
while (j<n_dimensions and s<=1):
s+=p[j]**2
j+=1
#comprobar si el punto esta contenido en la n-esfera
if (s<=1):
hits += 1
#devolver volumen de la n-esfera
return (2**n_dimensions)* float(hits) / n_points
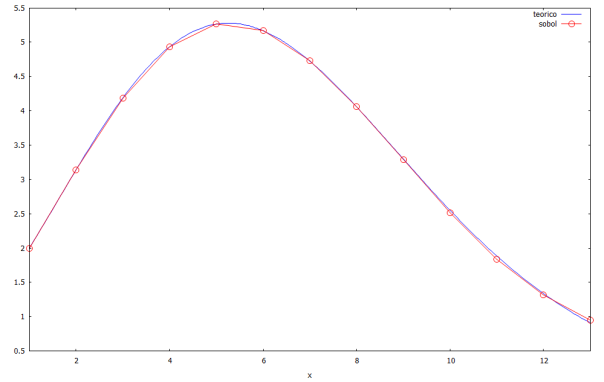
Y los resultados comparados con el volumen dado por la fórmula:
Voi-lá, podemos ver cómo el método Monte Carlo se acerca a la función que describe el volumen de la n-esfera. Aquí están los datos obtenidos para 1.000.000 de puntos lanzados para las distintas dimensiones:
| dimensiones | volumen n-cubo | volumen n-esfera | Monte Carlo | Puntos dentro |
| 1 | 2 | 2,000000 | 2,000000 | 1000000 |
| 2 | 4 | 3,141593 | 3,141700 | 785425 |
| 3 | 8 | 4,188790 | 4,188096 | 523512 |
| 4 | 16 | 4,934802 | 4,936320 | 308520 |
| 5 | 32 | 5,263789 | 5,263712 | 164491 |
| 6 | 64 | 5,167713 | 5,174656 | 80854 |
| 7 | 128 | 4,724766 | 4,734080 | 36985 |
| 8 | 256 | 4,058712 | 4,066048 | 15883 |
| 9 | 512 | 3,298509 | 3,289088 | 6424 |
| 10 | 1024 | 2,550164 | 2,516992 | 2458 |
| 11 | 2048 | 1,884104 | 1,837056 | 897 |
| 12 | 4096 | 1,335263 | 1,314816 | 321 |
| 13 | 8192 | 0,910629 | 0,950272 | 116 |
El número de puntos que cumplen las condiciones de la n-esfera disminuye con el número de dimensiones, pero a la vez aumenta el volumen del n-cubo en el que está circunscrita. La relación máxima entre los puntos «acertados» y los lanzados respecto al volumen del n-cubo se da cuando llegamos a cinco dimensiones, y a partir de ahí el volumen de la n-esfera empezará a converger hacia cero.
Otra consideración a tener en cuenta es que cada vez que aumentamos una dimensión, el volumen del n-cubo aumenta. Como consecuencia, la muestra de 1.000.000 de puntos es menos significativa, por lo que los resultados empeoran si no aumentamos el número de puntos aleatorios utilizados.
Esta entrada participa en la 3.141592653 Edición del Carnaval de Matemáticas que aloja Que no te aburran las M@tes.
Esta entrada participó en el Carnaval y lo ganó, porque los informáticos que estudiamos física a veces les caemos bien a los matemáticos 😛

Precioso, ¿verdad?
Referencias y enlaces de interés
Código fuente usado para realizar las pruebas
¿Cuál es el volumen de la bola unidad de dimensión N? en Gaussianos
Implementación de Sobol en Python
Publicado el diciembre 19, 2012 en Algorítmos, Python y etiquetado en hiperesfera, método monte carlo, monte-carlo, n-esfera, pi, pseudoaleatorio, python, sobol. Guarda el enlace permanente. 25 comentarios.





¿Sería posible saber cuánto te llevó hacer la simulación para 1kk puntos? Python es endiabladamente rápido pero estos cálculos le costará hacerlos hasta a él XD
Y al hilo de esta pregunta, me imagino que en la línea 19 usas un while para reducir el tiempo de ejecución. Sería interesante hacer una comparativa con algo como:
sum([x**2 for x in p])
o incluso math.fsum para mayor precisión (con un poco de suerte estará súper optimizada en C y será tan rápida como math.factorial e.e)
Saludines 🙂
Pues el while lo usé principalmente para ahorrarme sumas, pero es cuestión de probar con el otro método. Como no estaba buscando eficiencia no probé tiempos, pero ahora tengo el ordenador a 400km jeje, así que hasta dentro de unos días no te podré contestar bien. Puedo decirte que con cada dimensión el tiempo aumentaba bastante, pero no se si era por el cálculo de las coordenadas sobol o por las sumas. En cuanto pueda probarlo te lo comento
He aprovechado estos días para mirarme mejor python y numpy, soy todavía un novato en este lenguaje y me falta mucho para llegar a ser eficaz. Pero al final he dado con una solución más rápida. La ventaja es que el método que devuelve los números sobol los devuelve en formato array de numpy, así que puedo concatenar estas operaciones:
p = (p*2)-1
if (sum ( p*p )10 a veces gana el while
No sé si te he entendido bien XD ¿Entonces es más rápido el while o el sum?
Depende XD
Si trabajas con pocas dimensiones es más rápido hacer las operaciones con vectores y hacer un sum. A medida que empiezas a subir dimensiones, por el comportamiento del problema, el while va ganando puntos porque empieza a compensar con las sumas y multiplicaciones que te dejas por el camino
Si te vas a 15 dimensiones, por ejemplo, es muy probable que alcances el uno con unas pocas sumas, pero si utilizas el sum, aunque sea muy eficiente, hará las 15 sumas y multiplicaciones.
Es más, se podría mejorar el código que usa el while incluyendo también el cambio de [0:1] a [-1:1] de las coordenadas.
Resumiendo: el sum es mucho más óptimo, pero en este problema en particular, llegados a un número de dimensiones importante te compensa ahorrarte operaciones con el while.
OH, vale XD Para serte sincero sólo leí el código por encima y no había caído en las posibles operaciones que te podías ahorrar con el while. ¿Qué tal un reduce? Nunca me gustó demasiado pero por probar:
p[0] = p[0]**2 # el primer elemento hay que elevarlo a mano u.u
s = reduce(lambda memo, current: memo if memo >= 1 else memo + current**2, p)
Vale que no se para igual que el while, pero a lo mejor este está más optimizado. Benchmarks, benchmarks everywhere XD
Impresiona la velocidad de convergencia utilizando la secuencia de Sobol. Con la uniforme bidimensional todo es mucho más lento, tanto con aleatorios puros como con pseudo-aleatorios. Muy elegante la integración con Geogebra. Me ha encantado el artículo 😀
Gracias Manuel. La verdad es que hasta que no haces la prueba no te crees que la diferencia en la convergencia sea tan importante.
Enhorabuena por el premio del carnaval de matematicas!!! Por si sirve de ayuda, tengo una entrada sobre cómo visualizar la esfera tridimensional S^3, espero que aclare algo 🙂
Gracias Moebius. Había visto modelos de ese tipo, pero por ejemplo el hipercubo me cuesta mucho menos intentar concebirlo que la hiperesfera, tengo un bloqueo mental ahí que me deja empanado cada vez que intento pensar como puede ser XD. Me ha gustado mucho la parte de visión de película, nunca lo había pensado desde ese punto de vista.
Hola , perdón que te moleste ¡Cómo puedo cambiar éste codigo a foxpro?
I go to see every day a few web sites and blogs to
read content, however this webpage provides quality based posts.
Pingback: Monte Carlo « El zombi de Schrödinger
Pingback: Y mientras tanto en el escriba matemático « El zombi de Schrödinger
Pingback: Viaje locuelo a otras dimensiones con Monte Carlo | Mates_mv | Scoop.it
Pingback: Resumen 28 edición Carnaval Matemáticas 3.141592653 « Que no te aburran las M@TES
Pingback: Viaje locuelo a otras dimensiones con Monte Carlo
Pingback: Bitacoras.com
Pingback: Ganador del Carnaval Matematicas Diciembre 2012 « Que no te aburran las M@TES
Pingback: Salinas, ¡la vida puede ser maravillosa! « El zombi de Schrödinger
Pingback: Premio Carnaval de Matemáticas Diciembre 2012 | Es Ciencia Online
Pingback: Anónimo
Pingback: Nueva temporada | El zombi de Schrödinger
Pingback: Viaje locuelo a otras dimensiones con Monte Carlo | El zombi de Schrödinger
Pingback: 📏 ¿Por qué no se puede medir la longitud de costa?