Curvas paramétricas y animaciones en Geogebra
Si tuvisteis la oportunidad de ver el artículo Rondando voy en el zombi de Schrödinger, habréis visto una serie de animaciones para explicar la condición de rodadura. Hoy voy a explicar como se pueden hacer estas animaciones gracias a Geogebra. En este caso partícular usaré la versión 4.2 de la herramienta, explicaré como se animan curvas paramétricas en esta herramienta y finalmente enlazaré a la animación completa en Geogebratube para que podáis disponer de ella.
¿hipnótico verdad?
Curvas paramétricas.
Para seguir esta primera parte de la explicación puedes descargarte el fichero Geogebra usado aquí.
Para empezar tenemos que hablar de curvas paramétricas en Geogebra. Su uso es muy sencillo una vez conoces la base. Para tener una curva paramétrica en dos dimensiones necesitamos dos funciones, una función para x y otra para y, ambas en función de un parámetro común t, así que el primer paso será la creación de estas funciones.
Para crear las funciones basta con situarnos en el campo de entrada de geogebra e introducir las funciones una a una:
Puede verse f(x) definida y g(x) definiéndose en el cuadro de comandos.
Ahora podréis ver en la lista de elementos que tenéis vuestras dos funciones definidas. Vamos a crear la curva paramétrica a partir de ellas. Para ello ocultamos primero las dos funciones creadas, nos situamos de nuevo en el campo de entrada e introducimos el siguiente comando:
Curva[f(t),g(t),t,0,2π]
Esta orden indica a Geogebra que tiene que crear una curva paramétrica con las funciones f y g como entrada para los valores (x,y), el parámetro común a ambas será t y estará definido entre 0 y 10. Veamos que pasa en Geogebra cuando definimos esta curva:
Si alguna vez habéis hecho prácticas con un osciloscopio o habéis estudiado combinaciones de ondas en dos dimensiones seguro que os suena esta figura de Lissajous.
Podéis ver por un lado las funciones definidas a las que les hemos desmarcado su opción de visibilidad y por otro lado la curva paramétrica (en este caso una figura de Lissajous) con el valor a.
Animando curvas.
¿Y cómo animo estas curvas? Hay una forma muy elegante de realizar la animación en Geogebra. Lo primero que haremos será crear un deslizador t_1, los límites del mismo serán 0 y 2*pi. Un deslizador es el elemento base para la animación en Geogebra, con estos elementos puedes variar el valor de un número y asociarlo a distintos elementos gráficos de forma que varíe su comportamiento.
Ahora solo tenemos que asociar el límite superior del parámetro que define el dominio para nuestra curva al valor del deslizador que hemos definido. De esta forma la curva se irá formando a medida que cambie el valor del deslizador. Para ello hacemos doble click sobre la curva y editamos su definición cambiando el 10 por t_1:
Curva[f(t), g(t), t, 0, t_1]
Para probarlo podemos mover el deslizador manualmente para ver como se crea la curva, o ponerlo en modo automático. Finalmente colocamos el deslizador en su posición inicial (importante para animar) y nos vamos al menú Archivo->exporta->Vista gráfica como gif animado
En el diálogo he seleccionado 100ms entre frames y he marcado que la animación sea un bucle, aquí podéis ver el resultado:
Puede verse como el valor t_1 oscila creando primero y eliminando después la curva en un bucle continuo.
Hay que tener en cuenta que Geogebra animará la parte de la pantalla que este visible en ese momento, por lo que antes de crear el gif animado deberéis ajustar la vista gráfica para que se adapte a vuestras necesidades.
Adornando las curvas.
Pero sería mejor si el dibujo tuviera algún elemento que nos ayudara a visualizar el movimiento de la curva. Para ello nos bastará con definir un punto que tenga como valores (x,y) las funciones definidas para nuestra curva paramétrica y como argumento para las mismas el valor del deslizador t_1. De nuevo nos dirigimos a la ventana de comandos y escribimos:
(f(t_1), g(t_1))
También podríamos crear un punto de la manera habitual y luego editarlo para poner los valores x,y deseados, sin embargo la ventana de comandos nos permite ahorrarnos muchos pasos.
Si a ese punto le añadimos dos segmentos que vayan desde los valores (f(t_1),0) y (0,g(t_1)) a nuestro punto, tendremos lo siguiente:
En esta ocasión t_1 ha sido ajustado para que sea incremental, es decir, su valor crece hasta alcanzar el máximo y vuelve al valor inicial.
Aquí podéis obtener, a través de geogebratube, la sencilla animación con la que he empezado las explicaciones.
Y la cicloide
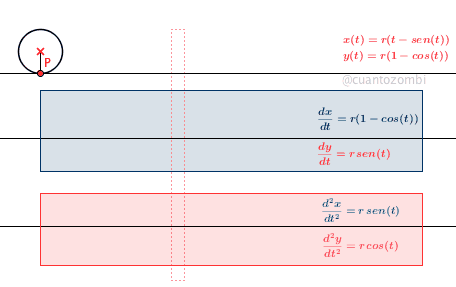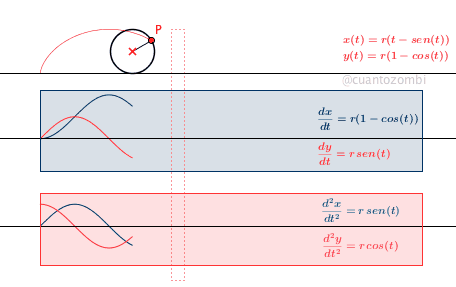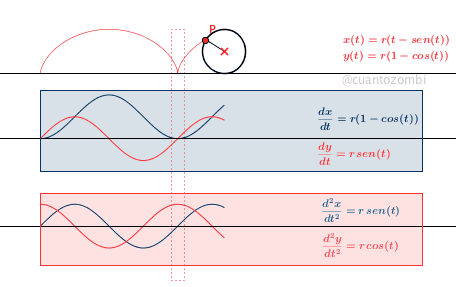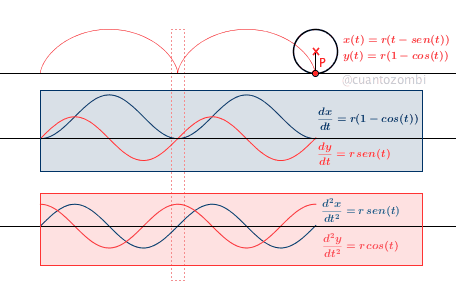
Tras las explicaciones con esta sencilla figura de Lissajous puedes imaginar como se creó la cicloide. Las funciones que se representan están escritas en la propia animación y se han creado con el mismo método que el usado anteriormente. La novedad en este caso es la rueda que va girando para crear la curva cicloide. En realidad la cicloide se dibuja normalmente y la rueda se mueve al mismo tiempo al estar fijada a un punto P que está definido según los valores x(t), y(t).
Si en un fichero de geogebra vacío introducís los siguientes comandos:
f(t) = t - sin(t) g(t) = 1-cos(t) d=deslizador[0,4*pi] O = (d,1) P = (f(d),g(d)) Curva[f(t), g(t), t, 0, d] Circunferencia[O, P] Segmento[O,P]
Tendréis la cicloide funcionando en cuanto modifiquéis los valores del deslizador d:
La cicloide sin adornos.
El resto de la animación es repetir lo aprendido, solo tenéis que crear las funciones para las derivadas de primer orden y segundo orden y pintarlas en sus posiciones correspondientes y adornar con cuadros sombreados, colores y algunos cuadros de texto en los que poner la fórmulas correspondientes. Vamos, lo que siempre se dice que son los remates finales, pero que al final te llevan más tiempo que la parte interesante de la animación ;P.
Finalmente aquí tenéis el fichero fuente de la animación subido en Geogebratube, para que podáis visualizarlo, descargarlo y jugar con él. Y si tenéis cualquier duda al respecto, aquí me tenéis.
PD: La animación es mejorable, pero no me detuve a optimizarla en su momento y seguro que hay objetos definidos sin uso o asesinatos de moscas con cañonazos como el uso de paramétricas para las velocidades y aceleraciones cuando bastaría con una función simple :P.
Viaje locuelo a otras dimensiones con Monte Carlo
Hace poco publiqué una entrada sobre los métodos Monte Carlo en El zombi de Schrödinger, entrada que tuvo su réplica en El escriba matemático, explicando la pequeña locura que fue mezclar Python y Geogebra 5 en fase beta. De estos dos posts surgió esta animación de cálculo del número PI:
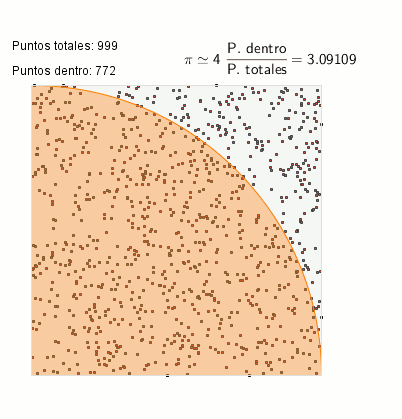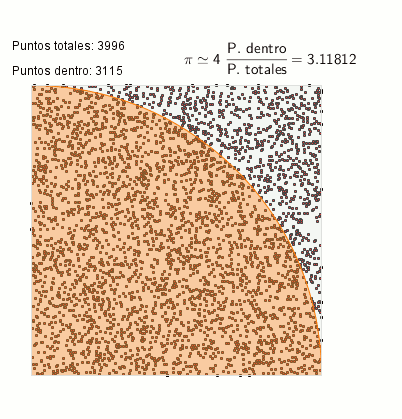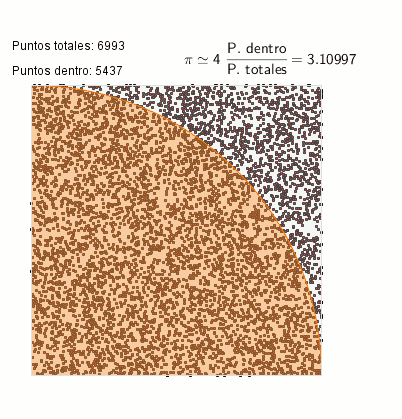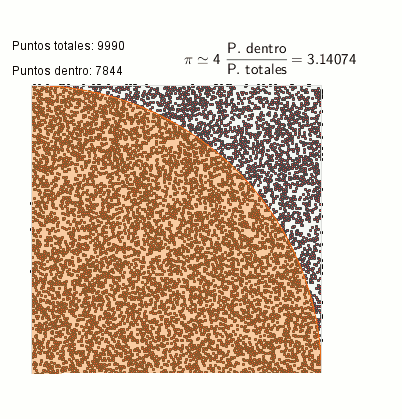
Cálculo de PI mediante el método Monte-Carlo
Pero ¿se puede afinar más en la búsqueda del número PI por este método? La respuesta es un SÍ rotundo. Una característica importante a la hora de ejecutar un método Monte Carlo es realizar una buena elección del generador de números aleatorios, cosa que no hice.
El cálculo de PI es un ejemplo de integración mediante método Monte Carlo: calculamos el área del sector del círculo y, gracias a la relación entre el área de ese sector y del cuadrado que lo contiene, obtenemos la aproximación de PI.
El área del cuadrado será
y el área del sector será
Si dividimos el área del círculo por el área del sector, tendremos:
Si realizamos la división del número total de puntos que tenemos dentro del círculo respecto al número total de puntos que se han señalado en toda la área del cuadrado, tendremos una aproximación del valor de π
En este tipo de problemas, un buen generador de números aleatorios será aquel que consiga cubrir el espacio estudiado lo más homogéneamente posible. De esta forma, habrá más probabilidad de que la razón entre el total de puntos lanzados y los puntos dentro de nuestro objeto sea similar a la razón real entre el volumen de nuestro campo de pruebas y el objeto circunscrito que deseamos medir.
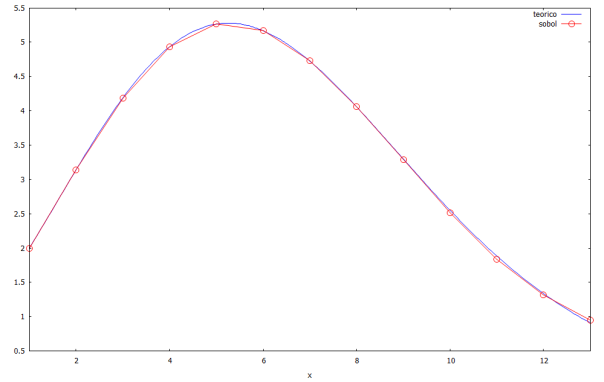
Investigando el tema, descubrí un generador de números pseudoaleatorios llamado secuencia de Sobol (más información aquí) y que distribuye puntos de una forma muy homogénea a lo largo de las dimensiones que elijamos. A continuación, un ejemplo de una distribución de puntos obtenida uniformemente y otra obtenida mediante una secuencia Sobol:
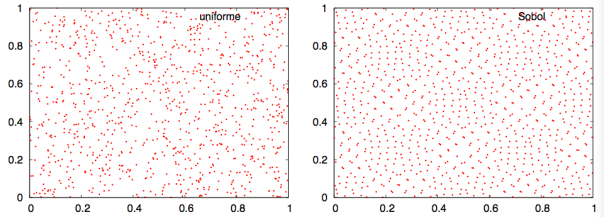
Comparativa de la generación de 1000 puntos aleatorios mediante el generador uniforme de python y la secuencia Sobol
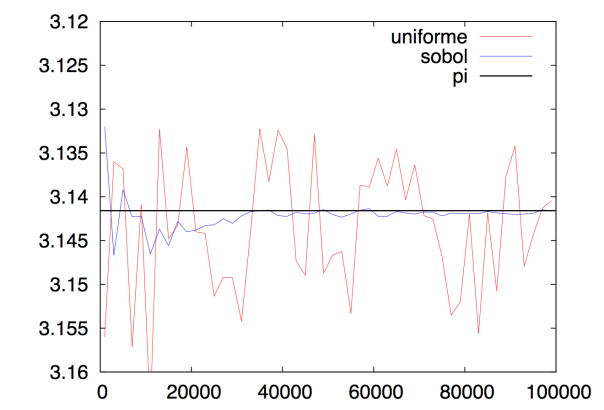
Lo siguiente fue comprobar si realmente se notaba la diferencia al realizar el cálculo de PI usando un método u otro. Aquí tenéis la comparación del cálculo de PI con un generador uniforme de números aleatorios y con un generador de secuencias Sobol:
- Cálculo de pi mediante distintos tipos de generadores de números aleatorios.
El cálculo se realizó para distintos números de puntos lanzados, hasta un máximo de 100.000 puntos. Se puede ver con claridad la mejora que produce el uso de una secuencia Sobol (azul) respecto a un generador de números aleatorios uniforme. La convergencia hacia el valor de PI es muy evidente cuando usamos secuencias Sobol. Para ver el código fuente usado puedes ir a la parte final.
¿Por qué conformarnos solo con dos dimensiones?
Poco después descubrí un enlace a un artículo ya con solera de Gaussianos:
¿Cuál es el volumen de la bola unidad de dimensión N?
Grosso modo lo que nos cuenta es el particular comportamiento del volumen de una esfera de radio 1 a medida que aumentamos el número de dimensiones. Podemos ver cómo en principio el volumen aumenta con el número de dimensiones para luego decrecer, tendiendo hacia cero a medida que aumentamos n. La fórmula para el volumen de una n-esfera de radio 1 es:
La explicación es bastante lógica; para que un punto del espacio de n-dimensiones se encuentre dentro de la n-esfera de radio 1 correspondiente, debe cumplir que su distancia al origen sea menor o igual a 1, y a medida que aumentamos las dimensiones llega un momento en el que es muy difícil encontrar puntos que cumplan esta condición, ya que para cada dimensión tenemos que sumar el cuadrado de un nuevo término.
La fórmula para saber si un punto está dentro de una n-esfera es:
La rabia del asunto es que es imposible visualizar una n-esfera de más de tres dimensiones dentro de un cubo, a su vez, de n-dimensiones. Quizás sea imposible imaginarlo, pero una computadora sí que puede ayudarnos a hacer algo similar: podemos calcular aproximadamente el volumen de una n-esfera de la misma forma que hicimos antes con el área de un círculo. Así que toca lanzar n-puntos a cascoporro para meter el dedo en la yaga y ver si todo esto es cierto.
Para cada dimensión, el cálculo del volumen de la n-esfera de radio 1 será el siguiente:
Siendo el volumen del n_cubo: 
El código para realizar el cálculo sería el siguiente:
#Calculo del volumen de una n-esfera. Como parametro recibe el numero de dimensiones y de puntos a generar, como salida devuelve el volumen
def calc_n_sphere_sobol(n_dimensions, n_points):
#numero de puntos dentro de la n-esfera
hits = 0
#inicializador de la secuencia sobol
sout = random.randint(1,10000)
for i in range(0, n_points):
#generar punto n-dimensional
p, sout = sobol_lib.i4_sobol ( n_dimensions, sout )
#transforma el numero del intervalo [0,1] al intervalo [-1,1]
p = (p*2)-1
j = 0
s = 0
#sumar cuadrado de las componentes
while (j<n_dimensions and s<=1):
s+=p[j]**2
j+=1
#comprobar si el punto esta contenido en la n-esfera
if (s<=1):
hits += 1
#devolver volumen de la n-esfera
return (2**n_dimensions)* float(hits) / n_points
Y los resultados comparados con el volumen dado por la fórmula:
Cálculo del espacio ocupado por una n-esfera de radio 1 para distintas dimensiones
Voi-lá, podemos ver cómo el método Monte Carlo se acerca a la función que describe el volumen de la n-esfera. Aquí están los datos obtenidos para 1.000.000 de puntos lanzados para las distintas dimensiones:
| dimensiones | volumen n-cubo | volumen n-esfera | Monte Carlo | Puntos dentro |
| 1 | 2 | 2,000000 | 2,000000 | 1000000 |
| 2 | 4 | 3,141593 | 3,141700 | 785425 |
| 3 | 8 | 4,188790 | 4,188096 | 523512 |
| 4 | 16 | 4,934802 | 4,936320 | 308520 |
| 5 | 32 | 5,263789 | 5,263712 | 164491 |
| 6 | 64 | 5,167713 | 5,174656 | 80854 |
| 7 | 128 | 4,724766 | 4,734080 | 36985 |
| 8 | 256 | 4,058712 | 4,066048 | 15883 |
| 9 | 512 | 3,298509 | 3,289088 | 6424 |
| 10 | 1024 | 2,550164 | 2,516992 | 2458 |
| 11 | 2048 | 1,884104 | 1,837056 | 897 |
| 12 | 4096 | 1,335263 | 1,314816 | 321 |
| 13 | 8192 | 0,910629 | 0,950272 | 116 |
El número de puntos que cumplen las condiciones de la n-esfera disminuye con el número de dimensiones, pero a la vez aumenta el volumen del n-cubo en el que está circunscrita. La relación máxima entre los puntos «acertados» y los lanzados respecto al volumen del n-cubo se da cuando llegamos a cinco dimensiones, y a partir de ahí el volumen de la n-esfera empezará a converger hacia cero.
Otra consideración a tener en cuenta es que cada vez que aumentamos una dimensión, el volumen del n-cubo aumenta. Como consecuencia, la muestra de 1.000.000 de puntos es menos significativa, por lo que los resultados empeoran si no aumentamos el número de puntos aleatorios utilizados.
Esta entrada participa en la 3.141592653 Edición del Carnaval de Matemáticas que aloja Que no te aburran las M@tes.
Esta entrada participó en el Carnaval y lo ganó, porque los informáticos que estudiamos física a veces les caemos bien a los matemáticos 😛
Precioso, ¿verdad?
Referencias y enlaces de interés
Código fuente usado para realizar las pruebas
¿Cuál es el volumen de la bola unidad de dimensión N? en Gaussianos
Implementación de Sobol en Python
GeoGebra 5, Python y Monte Carlo
La gran novedad de GeoGebra 5 es la posibilidad de usar un modo 3d, pero no dejéis que os ciegue esa importante mejora, porque hay otras. En la versión 5 del programa encontramos una nueva funcionalidad que va a permitir a GeoGebra convertirse en una herramienta de una potencia prácticamente ilimitada. Se trata de la integración con Python.
Lee el resto de esta entrada
Las bondades de máxima y un ejemplo para el cálculo de diferencias divididas
Aunque máxima no es mi herramienta favorita, hay que reconocer que en ocasiones su inmediatez lo hace muy útil. En este caso os traigo un rápido desarrollo para calcular una tabla de diferencias divididas, en parte gracias a una de las mejores utilidades que ofrece máxima: makelist. Lee el resto de esta entrada
Crear comandos en LaTeX
Cuando se realiza documentación sobre resultados de laboratorio, las diferenciales toman el control de la documentación. A mi me gusta escribir los documentos de LaTeX a mano, pero no me gusta escribir de más, así que una de las primeras cosas que hice fue crearme mi propio comando para escribir diferenciales:
\providecommand{\diferencial}[2]{\frac{\partial #1}{ \partial #2}} Lee el resto de esta entrada
El escriba matemático 